Análisis de Componentes Principales
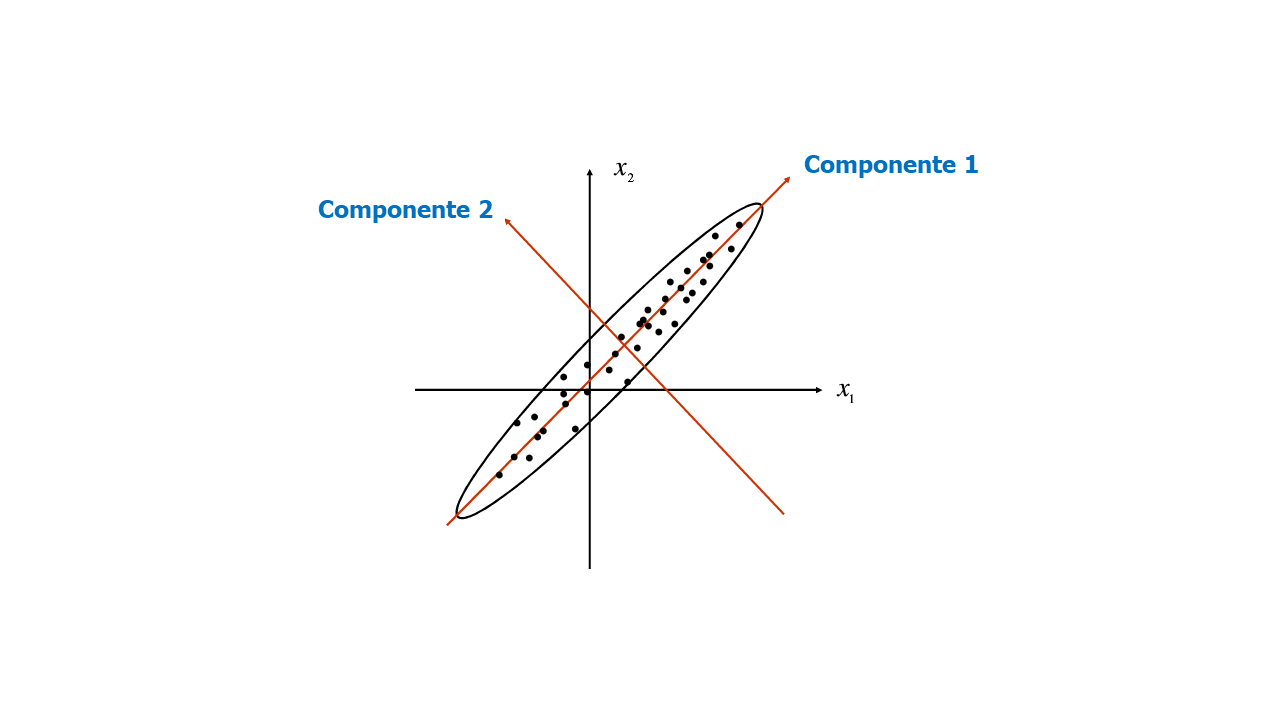
Suponga que tenemos una base de datos con cinco variables, cada variable es una dimensión, entonces tenemos cinco dimensiones. Con la herramienta de Análisis de Componentes Principales (ACP) o en inglés Principal Components Analysis (PCA) podemos reducir la dimensionalidad de la base de datos, por ejemplo, a dos dimensiones. Con el ACP se logra que estas dos nuevas variables puedan resumir la mayor proporción de la variabilidad de la información original. Estas nuevas variables se llaman Componentes Principales. La siguiente figura muestra cómo las variables originales se pueden expresar en dos nuevos ejes llamados Componente 1 y Componente 2; sin embargo, el Componente Principal 1 es el más importante porque que recoge más información. Este análisis se realiza con la matriz de varianzas-covarianzas del conjunto de datos.
Componentes
Los Componentes Principales son los Eigenvectores de la matriz de varianzas-covarianzas de las variables originales y se convertirán en los nuevos ejes. El ángulo entre los Eigenvectores es de 90°, así que los Eigenvectores son ortogonales entre sí.
La matriz de varianzas-covarianzas es simétrica, del orden \(nxn\), las varianzas, \((\sigma^2_{ij})\), de cada variable están en la diagonal de la matriz, los demás valores son las covarianzas, \((\sigma_{ij})\).
Para \(p\) variables, se extraen \(p\) Eigenvectores y \(p\) Eigenvalores. Estos Eigenvectores son las Componentes Principales y el Eigenvector asociado a cada Componente Principal es la proporción de la varianza total que ese componente puede explicar.
En el ACP no se generan variables nuevas, sino que se transforman en nuevas combinaciones lineales. Por lo anterior, la varianza total de las variables originales sigue siendo la misma.
Técnicamente, el Análisis de Componentes Principales implica la rotación del sistema de coordenadas original a un nuevo sistema de coordenadas con propiedades estadísticas inherentemente deseables. Más precisamente, buscamos definir una transformación ortogonal a una matriz de covarianza diagonal. Computacionalmente, ACP se reduce a resolver los valores propios y los vectores propios de una matriz definida positiva mediante un proceso generalmente denominado análisis de valores propios o descomposición espectral.
Ejemplo:
Supongamos la siguiente matriz de varianzas-covarianzas de un conjunto de dos variables:
La varianza de la variable 1 es igual a 0,00761 y la varianza de la variable 2 es 0,00840. La sumatoria de la varianza del conjunto de datos es de 0,01601 \((0,00761+0,00840)\).
Eigenvalores:
Eigenvalores \(\lambda_i\): varianzas de cada Componente.
El Componente Principal 1 es el más importante porque es el de mayor Eigenvalor. Los Eigenvalores son las varianzas de cada Componente Principal y la suma de los Eigenvalores es la suma de las varianzas de las variables originales, es decir, es la varianza total, la cual es 0,01601 \((0,0113385+0,00467151)\).
El Componente Principal 1 explica el 70,82% de la variabilidad total. Recuerde que la sumatoria de los \(\lambda\) es igual a la sumatoria de las varianzas de las variables. El analista puede decidir en trabajar solo con esta Componente y así se reduciría la dimensionalidad de los datos. Este es el objetivo del ACP, encontrar la menor cantidad de componentes posibles que puedan explicar la mayor parte de la variación original. En otras palabras, con el ACP se busca representar la \(p\) variables en un número menor de variables (Componentes) conformadas como combinaciones lineales de las originales y perder la menor cantidad de información.
Al aplicar el ACP, las variables originales correlacionadas se transforman en variables no correlacionadas.
Proporción de la varianza de la Componente Principal 1:
Proporción de la varianza de la Componente Principal 2:
Como la desviación estándar es la raíz cuadrada de la varianza, cada Componente Principal tiene la siguiente desviación estándar.
Desviación estándar Componente Principal 1:
Desviación estándar Componente Principal 2:
Eigenvectores:
Eigenvectores: Cargas de cada Componente.
Las cargas de un Componente Principal son los elementos del vector propio que forman la componente. Cada componente es una combinación lineal de las variables del conjunto de datos.
El primer elemento de \(Eigenvector_1\) es 0,6638921, esta es la carga o score para la primera variable original. El segundo elemento es la carga que se le asigna a la segunda variable de la base de datos.
A la matriz que se conforma con los Eigenvectores se llama matriz de rotación.
Cada vector propio debe tener una longitud igual a 1,0. Esto se comprueba si la suma de cada elemento (cargas) al cuadrado es igual a 1,0. Esta condición es una restricción del modelo porque con el valor de 1,0 las varianzas no se modifican.
Unidades de las variables:
Cuando se tienen variables con magnitudes grandes y otras pequeñas, se tiene un problema porque las variables de magnitud mayor van a predominar en la reducción de dimensionalidad y además, estas variables tienen mayor varianza. También, la covarianza entre las variables será mayor por la magnitud, siendo esto en muchos casos un resultado errado porque la covarianza estaría afectada por las unidades de las variables con unidades mayores y no por el co-movimiento.
Para solucionar esto tenemos dos opciones:
1. Cambio de escala de las variables: puede cambiar las unidades de cada variable con una de las siguientes dos opciones:
2. Matriz de correlaciones: realizar el ACP sobre la matriz de coeficientes de correlación en lugar de la matriz de varianzas-covarianzas.
Como la diagonal tiene valores de 1,0, la suma de la diagonal es igual a \(p\), cantidad de variables.
Matriz de varianzas-covarianzas del ejemplo:
A = matrix(c(0.00761, 0.00331, 0.00331, 0.00840), ncol = 2)
print(A)
[,1] [,2]
[1,] 0.00761 0.00331
[2,] 0.00331 0.00840
Eigenvalores e Eigenvectores:
eigen = eigen(A)
print(eigen)
eigen() decomposition
$values
[1] 0.011338485 0.004671515
$vectors
[,1] [,2]
[1,] 0.6638921 -0.7478284
[2,] 0.7478284 0.6638921
\(\lambda_1\): varianza de la Componente Principal 1.
lambda_1 = eigen$values[1]
print(lambda_1)
[1] 0.01133849
\(\lambda_2\): varianza de la Componente Principal 2.
lambda_2 = eigen$values[2]
print(lambda_2)
[1] 0.004671515
PC1: cargas de la Componente Principal 1.
pc1 = eigen$vectors[c(1,2)]
print(pc1)
[1] 0.6638921 0.7478284
PC2: cargas de la Componente Principal 2.
pc2 = eigen$vectors[c(3,4)]
print(pc2)
[1] -0.7478284 0.6638921
Prueba:
La suma de las cargas de cada componente al cuadrado debe ser igual a 1,0:
print(sum(pc1^2))
[1] 1
print(sum(pc2^2))
[1] 1
Si los vectores son ortogonales, entonces el producto escalar de los vectores es igual a cero:
print(pc1 %*% pc2)
[,1]
[1,] 0
\(\sum{\lambda_i} = \sum{var_i}\): la suma de las varianzas de las variables es igual a la suma de los Eigenvalores.
lambda_1 + lambda_2
A[1,1] + A[2,2]
Ejemplo ACP con EAM 2019:
datos <- read.csv("EAM_2019.csv", sep = ";", dec = ",", header = T)
print(head(datos))
ï..ciiu personal_mujer personal_hombre gasto_personal gasto_financiero
1 1051 36 140 9352991 3240559
2 1030 40 176 7334998 1468298
3 3290 15 172 6668544 1547666
4 3091 88 373 22088759 35203208
5 3290 18 53 5219070 2861773
6 3290 18 53 5219070 2861773
costos_gastos_produccion gastos_adm_ventas inversion_AF ventas
1 6846304 22920307 4979745 192609248
2 5941761 12310286 5615593 115741258
3 6996020 2564695 773444 44580029
4 4175751 171278876 10501572 162509864
5 11037978 13691919 6423171 87324374
6 11037978 13691919 6423171 87324374
datos <- datos[, 2:9]
print(head(datos))
personal_mujer personal_hombre gasto_personal gasto_financiero
1 36 140 9352991 3240559
2 40 176 7334998 1468298
3 15 172 6668544 1547666
4 88 373 22088759 35203208
5 18 53 5219070 2861773
6 18 53 5219070 2861773
costos_gastos_produccion gastos_adm_ventas inversion_AF ventas
1 6846304 22920307 4979745 192609248
2 5941761 12310286 5615593 115741258
3 6996020 2564695 773444 44580029
4 4175751 171278876 10501572 162509864
5 11037978 13691919 6423171 87324374
6 11037978 13691919 6423171 87324374
Matriz de varianzas-covarianzas:
A = cov(datos)
print(A)
personal_mujer personal_hombre gasto_personal
personal_mujer 3.739215e+04 1.997898e+04 1.862377e+09
personal_hombre 1.997898e+04 5.062854e+04 3.599630e+09
gasto_personal 1.862377e+09 3.599630e+09 3.545755e+14
gasto_financiero 5.104016e+07 7.252934e+07 1.365787e+13
costos_gastos_produccion 1.221006e+09 2.766463e+09 3.967152e+14
gastos_adm_ventas 2.949389e+09 1.403570e+10 2.183437e+15
inversion_AF 1.108302e+09 2.779767e+09 2.928899e+14
ventas 4.820786e+09 3.646053e+10 5.053759e+15
gasto_financiero costos_gastos_produccion
personal_mujer 5.104016e+07 1.221006e+09
personal_hombre 7.252934e+07 2.766463e+09
gasto_personal 1.365787e+13 3.967152e+14
gasto_financiero 1.967009e+13 2.705401e+13
costos_gastos_produccion 2.705401e+13 1.209958e+15
gastos_adm_ventas 1.149462e+14 6.138182e+15
inversion_AF 4.619610e+13 8.194616e+14
ventas 1.874646e+14 1.326626e+16
gastos_adm_ventas inversion_AF ventas
personal_mujer 2.949389e+09 1.108302e+09 4.820786e+09
personal_hombre 1.403570e+10 2.779767e+09 3.646053e+10
gasto_personal 2.183437e+15 2.928899e+14 5.053759e+15
gasto_financiero 1.149462e+14 4.619610e+13 1.874646e+14
costos_gastos_produccion 6.138182e+15 8.194616e+14 1.326626e+16
gastos_adm_ventas 5.944858e+16 4.009155e+15 1.178659e+17
inversion_AF 4.009155e+15 1.547354e+16 8.777248e+15
ventas 1.178659e+17 8.777248e+15 2.478986e+17
eigen <- eigen(A)
eigen
eigen() decomposition
$values
[1] 3.056986e+17 1.516353e+16 2.811474e+15 5.205976e+14 1.924801e+14
[6] 1.831384e+13 2.326745e+04 1.157060e+04
$vectors
[,1] [,2] [,3] [,4] [,5]
[1,] -1.878137e-08 6.239123e-08 -1.183730e-07 -2.970771e-06 -6.900966e-06
[2,] -1.280982e-07 1.035893e-07 1.222791e-06 -2.739607e-06 -1.153716e-05
[3,] -1.807568e-02 7.757045e-03 9.011061e-02 -3.506543e-01 -9.312296e-01
[4,] -7.244017e-04 2.571890e-03 -7.326667e-03 -4.089698e-02 -2.462619e-02
[5,] -4.802479e-02 2.289081e-02 9.528623e-02 -9.260466e-01 3.601660e-01
[6,] -4.324727e-01 -2.931718e-02 -8.956921e-01 -8.763492e-02 -4.506920e-02
[7,] -3.333367e-02 9.989790e-01 -1.882518e-02 2.385429e-02 -1.764564e-03
[8,] -8.995680e-01 -2.430295e-02 4.244151e-01 9.776436e-02 2.123638e-02
[,6] [,7] [,8]
[1,] 2.949406e-06 9.999175e-01 -1.284377e-02
[2,] 2.607919e-06 -1.284377e-02 -9.999175e-01
[3,] 3.668912e-02 -7.412828e-06 1.200959e-05
[4,] -9.988294e-01 2.624774e-06 -2.251206e-06
[5,] 2.843181e-02 -3.586853e-07 -1.414615e-06
[6,] 1.150768e-02 -7.208121e-07 -2.435771e-07
[7,] 1.801331e-03 -1.123465e-08 4.458666e-08
[8,] -7.049896e-03 4.938902e-07 9.412163e-08
Eigenvalores:
Son las varianzas de las Componentes Principales.
lambda <- eigen$values
print(lambda)
[1] 3.056986e+17 1.516353e+16 2.811474e+15 5.205976e+14 1.924801e+14
[6] 1.831384e+13 2.326745e+04 1.157060e+04
Las desviaciones estándar de las Componentes Principales son:
sqrt(lambda)
- 552900143.548993
- 123140268.027212
- 53023338.9350048
- 22816608.8714465
- 13873720.756864
- 4279467.7380434
- 152.53671096197
- 107.566722167472
plot(lambda, type = "l")
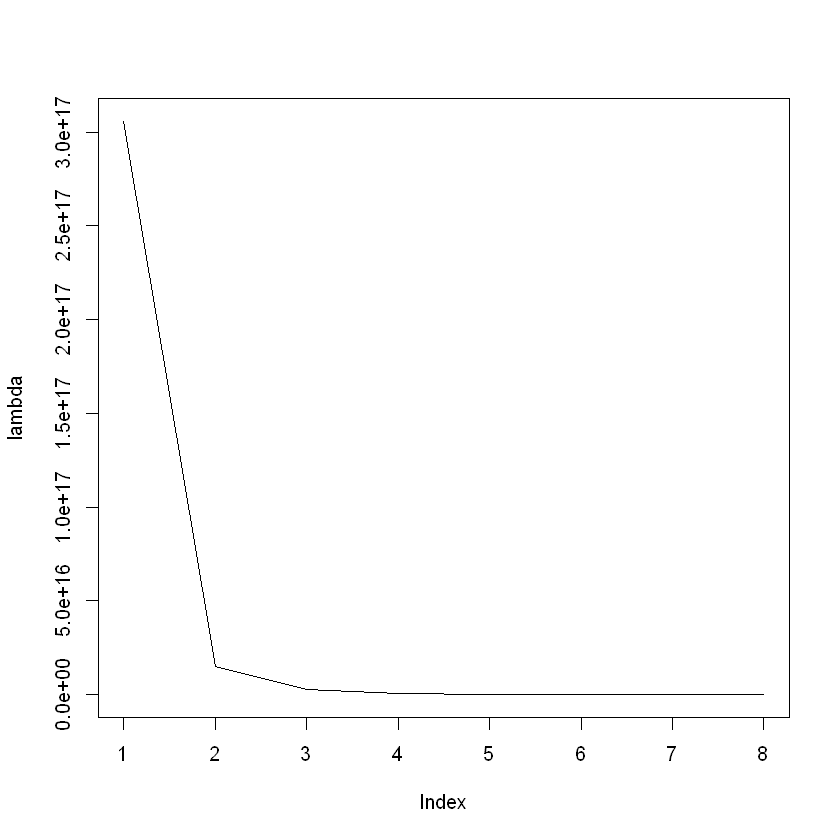
Problemas con las unidades de las variables:
La primera Componente Principal explica la mayor cantidad de la
variabilidad del conjunto de datos, pero tenemos un problema con las
unidades de las variables, tenemos dos variables personal_mujer y
personal_hombre con magnitudes mucho menores que las demás. Esto
significa que la primer Componente Principal está otorgando mayor
importancia a las variables de mayor magnitud. Para solucionar este
problema podemos cambiar la escala de las variables originales o aplicar
el ACP a la matriz de correlaciones. En esta sesión se aplicar a la
matriz de correlaciones.
Con este problema la técnica del codo indica que sólo se necesita una Componente Principal.
Eigenvectores:
Son las cargas de cada Componente Principal.
cargas <- eigen$vectors
print(cargas)
[,1] [,2] [,3] [,4] [,5]
[1,] -1.878137e-08 6.239123e-08 -1.183730e-07 -2.970771e-06 -6.900966e-06
[2,] -1.280982e-07 1.035893e-07 1.222791e-06 -2.739607e-06 -1.153716e-05
[3,] -1.807568e-02 7.757045e-03 9.011061e-02 -3.506543e-01 -9.312296e-01
[4,] -7.244017e-04 2.571890e-03 -7.326667e-03 -4.089698e-02 -2.462619e-02
[5,] -4.802479e-02 2.289081e-02 9.528623e-02 -9.260466e-01 3.601660e-01
[6,] -4.324727e-01 -2.931718e-02 -8.956921e-01 -8.763492e-02 -4.506920e-02
[7,] -3.333367e-02 9.989790e-01 -1.882518e-02 2.385429e-02 -1.764564e-03
[8,] -8.995680e-01 -2.430295e-02 4.244151e-01 9.776436e-02 2.123638e-02
[,6] [,7] [,8]
[1,] 2.949406e-06 9.999175e-01 -1.284377e-02
[2,] 2.607919e-06 -1.284377e-02 -9.999175e-01
[3,] 3.668912e-02 -7.412828e-06 1.200959e-05
[4,] -9.988294e-01 2.624774e-06 -2.251206e-06
[5,] 2.843181e-02 -3.586853e-07 -1.414615e-06
[6,] 1.150768e-02 -7.208121e-07 -2.435771e-07
[7,] 1.801331e-03 -1.123465e-08 4.458666e-08
[8,] -7.049896e-03 4.938902e-07 9.412163e-08
Proporción de la varianza de cada Componente Principal:
La varianza que cada Componente Principal logra explicar por separado:
prop_var <- lambda/sum(lambda)
print(prop_var)
[1] 9.423363e-01 4.674258e-02 8.666558e-03 1.604777e-03 5.933329e-04
[6] 5.645365e-05 7.172347e-14 3.566715e-14
Proporción de varianza acumulada al aumentar Componentes Principales:
prop_var_acum <- cumsum(lambda)/sum(lambda)
print(prop_var_acum)
[1] 0.9423363 0.9890789 0.9977454 0.9993502 0.9999435 1.0000000 1.0000000
[8] 1.0000000
La Componente Principal 1 explica el 94,23% de la varianza del conjunto de datos.
ACP con la matriz de correlaciones:
Se realiza el mismo procedimiento, pero con la matriz de coeficientes de correlación:
A = cor(datos)
print(A)
personal_mujer personal_hombre gasto_personal
personal_mujer 1.00000000 0.45918261 0.5114733
personal_hombre 0.45918261 1.00000000 0.8495829
gasto_personal 0.51147327 0.84958291 1.0000000
gasto_financiero 0.05951392 0.07267965 0.1635405
costos_gastos_produccion 0.18152747 0.35346147 0.6056747
gastos_adm_ventas 0.06255630 0.25583836 0.4755711
inversion_AF 0.04607581 0.09931522 0.1250418
ventas 0.05007149 0.32545296 0.5390426
gasto_financiero costos_gastos_produccion
personal_mujer 0.05951392 0.1815275
personal_hombre 0.07267965 0.3534615
gasto_personal 0.16354049 0.6056747
gasto_financiero 1.00000000 0.1753652
costos_gastos_produccion 0.17536517 1.0000000
gastos_adm_ventas 0.10629691 0.7237423
inversion_AF 0.08373504 0.1893863
ventas 0.08489441 0.7659955
gastos_adm_ventas inversion_AF ventas
personal_mujer 0.0625563 0.04607581 0.05007149
personal_hombre 0.2558384 0.09931522 0.32545296
gasto_personal 0.4755711 0.12504179 0.53904261
gasto_financiero 0.1062969 0.08373504 0.08489441
costos_gastos_produccion 0.7237423 0.18938634 0.76599555
gastos_adm_ventas 1.0000000 0.13218655 0.97091339
inversion_AF 0.1321865 1.00000000 0.14171846
ventas 0.9709134 0.14171846 1.00000000
eigen <- eigen(A)
eigen
eigen() decomposition
$values
[1] 3.56505893 1.52081291 1.02309043 0.91630483 0.55575693 0.30401093 0.09273024
[8] 0.02223479
$vectors
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] -0.2106928 -0.57578375 0.02214712 0.02361349 0.772202925 0.11726775
[2,] -0.3585481 -0.46745657 0.08352398 0.04828165 -0.542176918 0.14380998
[3,] -0.4548743 -0.32937778 0.04737869 -0.02403973 -0.253374106 -0.09286009
[4,] -0.1115576 -0.01348448 -0.74003083 -0.65388863 -0.021041260 0.09724572
[5,] -0.4461470 0.21007377 -0.01448462 -0.02746956 0.136769241 -0.82513357
[6,] -0.4336228 0.39544860 0.11741035 -0.03425391 0.155556129 0.41861887
[7,] -0.1238028 0.05636775 -0.64060409 0.75295144 -0.003127729 0.06144540
[8,] -0.4530927 0.37094199 0.13518240 -0.00996259 0.046822464 0.29601441
[,7] [,8]
[1,] -0.09769967 0.0586448480
[2,] -0.57271625 -0.0312928834
[3,] 0.77820633 -0.0578830139
[4,] -0.03932248 0.0266717602
[5,] -0.23007970 -0.0580479890
[6,] -0.04299362 -0.6628311912
[7,] 0.01999398 -0.0009877992
[8,] -0.01070724 0.7408130522
Eigenvalores:
Son las varianzas de las Componentes Principales.
lambda <- eigen$values
print(lambda)
[1] 3.56505893 1.52081291 1.02309043 0.91630483 0.55575693 0.30401093 0.09273024
[8] 0.02223479
Las desviaciones estándar de las Componentes Principales son:
sqrt(lambda)
- 1.88813636414594
- 1.23321243323159
- 1.01147932912133
- 0.957238127235179
- 0.745491067526704
- 0.551371866199051
- 0.304516400845997
- 0.149113361098913
screeplot(princomp(datos, cor = T),
main = "Screeplot", col = "blue", type = "lines",
pch = 19)
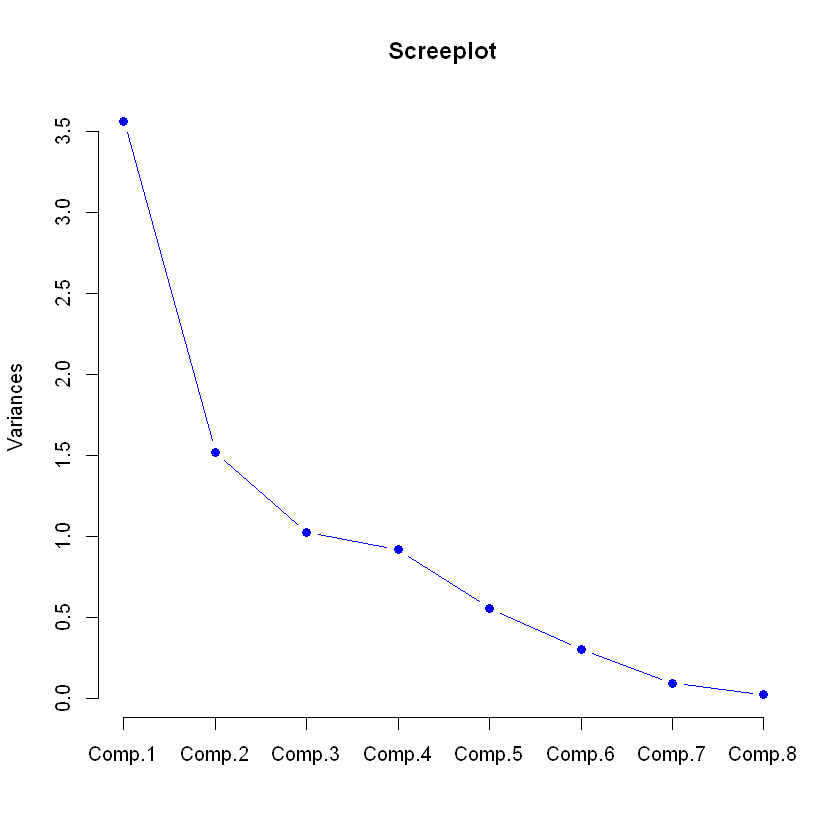
En otra sesión podrá comprobar que estos resultados con la matriz de correlación son igual que si se escalaran los datos.
En este resultado la técnica del codo ya no muestra que se debe seleccionar una sola Componente Principal. Se solucionó el problema de las unidades de las variables.
Eigenvectores:
Son las cargas de cada Componente Principal.
cargas <- eigen$vectors
print(cargas)
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] -0.2106928 -0.57578375 0.02214712 0.02361349 0.772202925 0.11726775
[2,] -0.3585481 -0.46745657 0.08352398 0.04828165 -0.542176918 0.14380998
[3,] -0.4548743 -0.32937778 0.04737869 -0.02403973 -0.253374106 -0.09286009
[4,] -0.1115576 -0.01348448 -0.74003083 -0.65388863 -0.021041260 0.09724572
[5,] -0.4461470 0.21007377 -0.01448462 -0.02746956 0.136769241 -0.82513357
[6,] -0.4336228 0.39544860 0.11741035 -0.03425391 0.155556129 0.41861887
[7,] -0.1238028 0.05636775 -0.64060409 0.75295144 -0.003127729 0.06144540
[8,] -0.4530927 0.37094199 0.13518240 -0.00996259 0.046822464 0.29601441
[,7] [,8]
[1,] -0.09769967 0.0586448480
[2,] -0.57271625 -0.0312928834
[3,] 0.77820633 -0.0578830139
[4,] -0.03932248 0.0266717602
[5,] -0.23007970 -0.0580479890
[6,] -0.04299362 -0.6628311912
[7,] 0.01999398 -0.0009877992
[8,] -0.01070724 0.7408130522
Proporción de la varianza de cada Componente Principal:
La varianza que cada Componente Principal logra explicar por separado:
prop_var <- lambda/sum(lambda)
print(prop_var)
[1] 0.445632366 0.190101613 0.127886304 0.114538104 0.069469616 0.038001367
[7] 0.011591280 0.002779349
Proporción de varianza acumulada al aumentar Componentes Principales:
prop_var_acum <- cumsum(lambda)/sum(lambda)
print(prop_var_acum)
[1] 0.4456324 0.6357340 0.7636203 0.8781584 0.9476280 0.9856294 0.9972207
[8] 1.0000000
La Componente Principal 2 explica el 44,56% de la varianza del conjunto de datos. Si se usan las dos primeras Componentes Principales, se puede explicar el 63,57% de la variabilidad total.
n <- dim(datos)[1]
mu <- colMeans(datos)
S <- cov(datos)
ones <- matrix(rep(1,n),nrow=n,ncol=1)
datos.cen <- as.matrix(datos) - ones %*% mu
datos.cen
Dx <- diag(diag(S))
head(Dx)
Y <- datos.cen %*% solve(Dx)^(1/2)
head(Y)
| personal_mujer | personal_hombre | gasto_personal | gasto_financiero | costos_gastos_produccion | gastos_adm_ventas | inversion_AF | ventas |
|---|---|---|---|---|---|---|---|
| -97.933333 | -120.55952 | -8848242 | 542927.8 | -8873424.4 | -47470381 | -15231998.3 | -9322297 |
| -93.933333 | -84.55952 | -10866235 | -1229333.2 | -9777967.4 | -58080402 | -14596150.3 | -86190287 |
| -118.933333 | -88.55952 | -11532689 | -1149965.2 | -8723708.4 | -67825993 | -19438299.3 | -157351516 |
| -45.933333 | 112.44048 | 3887526 | 32505576.8 | -11543977.4 | 100888188 | -9710171.3 | -39421681 |
| -115.933333 | -207.55952 | -12982163 | 164141.8 | -4681750.4 | -56698769 | -13788572.3 | -114607171 |
| -115.933333 | -207.55952 | -12982163 | 164141.8 | -4681750.4 | -56698769 | -13788572.3 | -114607171 |
| -90.933333 | -45.55952 | -8814568 | -2049686.2 | -10273889.4 | -65363031 | -19847471.3 | -168561472 |
| -110.933333 | -163.55952 | -13444970 | -2067063.2 | -14096981.4 | -57320166 | -19946718.3 | -142417492 |
| -25.933333 | -111.55952 | -7120020 | 17692642.8 | -13876201.4 | 2366699 | 30641843.7 | -175204156 |
| 63.066667 | -190.55952 | -9625892 | -2155495.2 | -11716938.4 | -46229220 | -19898921.3 | -144589296 |
| -81.933333 | -102.55952 | -14260980 | -2084792.2 | -14368440.4 | -69603180 | -14681641.3 | -178763412 |
| -116.933333 | -215.55952 | -16742030 | -1915841.2 | -15542454.4 | -6531891 | -19562703.3 | -183366258 |
| 1161.066667 | 215.44048 | 21415142 | 5065031.8 | 21992863.6 | 86146991 | -195466.3 | -9315245 |
| -60.933333 | -146.55952 | -13152689 | -1978187.2 | -14592572.4 | -45027116 | -19603064.3 | -179581278 |
| -80.933333 | -237.55952 | -14794075 | -622557.2 | -15552928.4 | -64743458 | -19564763.3 | -194943698 |
| -110.933333 | -156.55952 | -9868525 | -2179664.2 | 18939041.6 | -66312222 | -15047568.3 | -156986120 |
| 51.066667 | 25.44048 | -2844102 | -1782968.2 | -9814222.4 | -67894894 | -16759666.3 | -95440621 |
| 7.066667 | 511.44048 | 12759844 | -1210472.2 | 443689.6 | 39799286 | -7539531.3 | 34075337 |
| -76.933333 | -57.55952 | -9141983 | 886226.8 | -14470724.4 | -30447618 | -19356119.3 | -127418348 |
| 12.066667 | 158.44048 | 20332689 | 1353476.8 | -1422324.4 | -3301445 | 2807914.7 | 286147955 |
| -84.933333 | -168.55952 | -16265068 | -2069638.2 | -11517343.4 | -63226869 | -20211743.3 | -178577879 |
| -46.933333 | -141.55952 | -13589021 | -1950069.2 | -12632507.4 | -57588902 | -20202076.3 | -164060960 |
| 1.066667 | 15.44048 | -13400772 | -1829785.2 | -9649809.4 | -60713269 | -20211743.3 | -173608762 |
| -62.933333 | -97.55952 | -9692368 | -1773999.2 | -14878042.4 | -50459612 | -19270706.3 | -195283056 |
| -77.933333 | -90.55952 | -8516768 | 6776262.8 | 3476371.6 | -39909946 | -16764846.3 | 114463785 |
| -108.933333 | -113.55952 | -10875171 | -1828593.2 | -13506918.4 | -54520313 | -20031030.3 | -129990250 |
| -110.933333 | -150.55952 | -12177575 | -1043941.2 | -14889677.4 | -50791363 | -19273291.3 | -191691384 |
| -109.933333 | -44.55952 | -7748678 | -1615980.2 | -12747352.4 | -61044241 | -18588007.3 | -18847671 |
| -87.933333 | -128.55952 | -13241759 | -2154414.2 | -11183424.4 | -58557372 | -18885919.3 | -111318780 |
| -21.933333 | -139.55952 | -10693745 | -1884468.2 | -13144838.4 | -60072886 | -19430209.3 | -149442097 |
| ... | ... | ... | ... | ... | ... | ... | ... |
| 268.066667 | -159.55952 | -7198875 | -2025004.2 | -13735673.4 | -62277945.7 | -19336230 | -170872885 |
| -16.933333 | -152.55952 | -12164148 | -2001294.2 | -13040562.4 | -67402655.7 | -20143047 | -183896799 |
| 268.066667 | -159.55952 | -7198875 | -2025004.2 | -13735673.4 | -62277945.7 | -19336230 | -170872885 |
| 571.066667 | 847.44048 | 74882102 | -714230.2 | 617369.6 | 185608010.3 | -2427312 | 194835169 |
| 3.066667 | 110.44048 | 13856972 | -1866310.2 | 3498496.6 | -620021.7 | -14138976 | 159230907 |
| 571.066667 | 847.44048 | 74882102 | -714230.2 | 617369.6 | 185608010.3 | -2427312 | 194835169 |
| 12.066667 | 158.44048 | 20332689 | 1353476.8 | -1422324.4 | -3301444.7 | 2807915 | 286147955 |
| 571.066667 | 847.44048 | 74882102 | -714230.2 | 617369.6 | 185608010.3 | -2427312 | 194835169 |
| -80.933333 | -184.55952 | -10644577 | -840527.2 | -15268838.4 | -62801987.7 | -18719861 | -157385039 |
| 11.066667 | 77.44048 | 13820084 | -1913283.2 | -9614068.4 | -20322962.7 | -12564831 | 20434383 |
| -102.933333 | -162.55952 | -13456703 | -770210.2 | -11588523.4 | -56945757.7 | -8153748 | -91763885 |
| 11.066667 | 77.44048 | 13820084 | -1913283.2 | -9614068.4 | -20322962.7 | -12564831 | 20434383 |
| 11.066667 | 77.44048 | 13820084 | -1913283.2 | -9614068.4 | -20322962.7 | -12564831 | 20434383 |
| -109.933333 | -44.55952 | -7748678 | -1615980.2 | -12747352.4 | -61044240.7 | -18588007 | -18847671 |
| 13.066667 | 333.44048 | 11448329 | 5607969.8 | -132022.4 | -6603198.7 | -14709415 | 364658609 |
| 13.066667 | 333.44048 | 11448329 | 5607969.8 | -132022.4 | -6603198.7 | -14709415 | 364658609 |
| 13.066667 | 333.44048 | 11448329 | 5607969.8 | -132022.4 | -6603198.7 | -14709415 | 364658609 |
| -3.933333 | 227.44048 | 1017244 | -2076541.2 | -4092283.4 | -60230884.7 | -4736368 | -37928379 |
| 80.066667 | 116.44048 | 4903717 | 2787591.8 | 24698207.6 | -5611750.7 | 1442759179 | -2176733 |
| -93.933333 | -129.55952 | -12547871 | -2137565.2 | -13407820.4 | -66217952.7 | -19332931 | -150095075 |
| -55.933333 | -101.55952 | -7931405 | -2006407.2 | -14336425.4 | -49376649.7 | -8592027 | -146204442 |
| -120.933333 | -168.55952 | -15810979 | -2021662.2 | -15289081.4 | -67901462.7 | -19394784 | -189182927 |
| -120.933333 | -168.55952 | -15810979 | -2021662.2 | -15289081.4 | -67901462.7 | -19394784 | -189182927 |
| -111.933333 | -131.55952 | 3196088 | 24778103.8 | 12228515.6 | 154662468.3 | 1795539 | 31501235 |
| -105.933333 | -147.55952 | -4199323 | 5988384.8 | 5340003.6 | -30960090.7 | 4938570 | 177434155 |
| -97.933333 | -120.55952 | -8848242 | 542927.8 | -8873424.4 | -47470380.7 | -15231998 | -9322297 |
| 279.066667 | 252.44048 | 35732503 | -1804305.2 | -3548759.4 | -6290792.7 | -12337768 | 85603150 |
| 279.066667 | 252.44048 | 35732503 | -1804305.2 | -3548759.4 | -6290792.7 | -12337768 | 85603150 |
| -14.933333 | 49.44048 | 17418113 | -2186324.2 | 6092351.6 | 43264215.3 | -13912858 | 153602706 |
| -109.933333 | -44.55952 | -7748678 | -1615980.2 | -12747352.4 | -61044240.7 | -18588007 | -18847671 |
| 37392.15 | 0.00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0 | 0 |
| 0.00 | 50628.54 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0 | 0 |
| 0.00 | 0.00 | 3.545755e+14 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0 | 0 |
| 0.00 | 0.00 | 0.000000e+00 | 1.967009e+13 | 0.000000e+00 | 0.000000e+00 | 0 | 0 |
| 0.00 | 0.00 | 0.000000e+00 | 0.000000e+00 | 1.209958e+15 | 0.000000e+00 | 0 | 0 |
| 0.00 | 0.00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 5.944858e+16 | 0 | 0 |
| -0.5064543 | -0.5358014 | -0.4698970 | 0.12241620 | -0.2550975 | -0.1946937 | -0.12245090 | -0.01872345 |
| -0.4857687 | -0.3758070 | -0.5770650 | -0.27718287 | -0.2811017 | -0.2382094 | -0.11733929 | -0.17310964 |
| -0.6150542 | -0.3935841 | -0.6124579 | -0.25928744 | -0.2507934 | -0.2781797 | -0.15626560 | -0.31603404 |
| -0.2375405 | 0.4997180 | 0.2064519 | 7.32916782 | -0.3318718 | 0.4137801 | -0.07806062 | -0.07917682 |
| -0.5995399 | -0.9224545 | -0.6894340 | 0.03700974 | -0.1345932 | -0.2325428 | -0.11084712 | -0.23018378 |
| -0.5995399 | -0.9224545 | -0.6894340 | 0.03700974 | -0.1345932 | -0.2325428 | -0.11084712 | -0.23018378 |
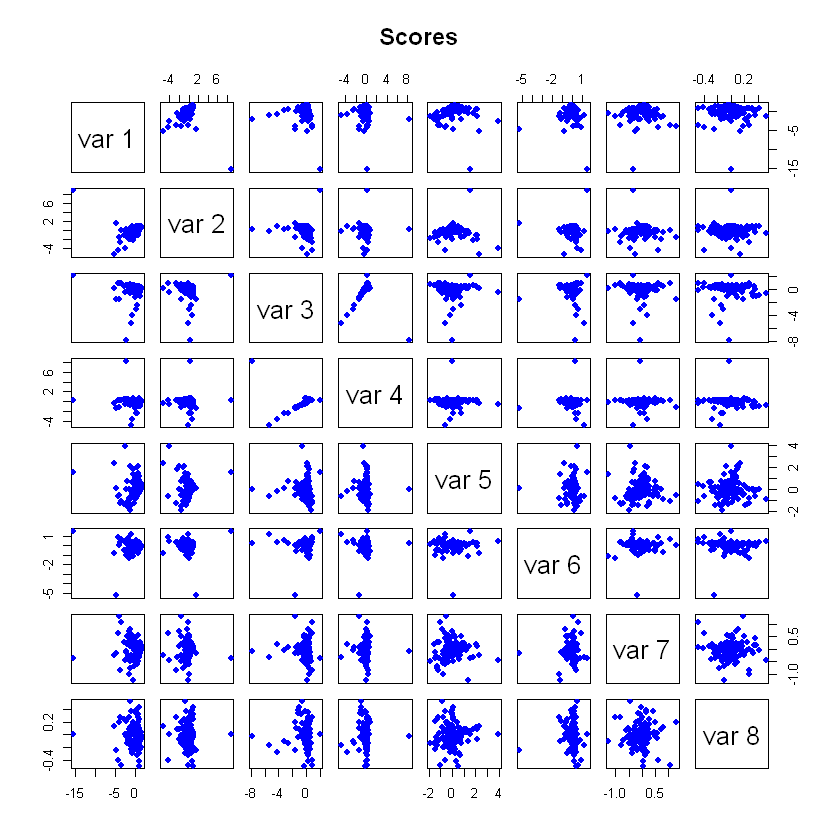
scores <- Y %*% cargas
pairs(scores,main="Scores",col="blue",pch=19)